Rh4_060713_SubDiv

---------SUBDIVISION SURFACES---------

In computer graphics, SUBDIVISION SURFACES are used to create smooth surfaces out of arbitrary meshes. Subdivision surfaces are defined as the limit of an infinite refinement process. They were introduced simultaneously by Edwin Catmull and Jim Clark, and by Daniel Doo and Malcom Sabin in 1978. Little progress was made until 1995, when Ulrich Reif solved subdivision surfaces behaviour near extraordinary vertices.

The fundamental concept is REFINEMENT. By repeatedly refining an initial polygonal mesh, a sequence of meshes is generated that converges to a resulting subdivision surface. Each new subdivision step generates a new mesh that has more polygonal elements and is smoother.



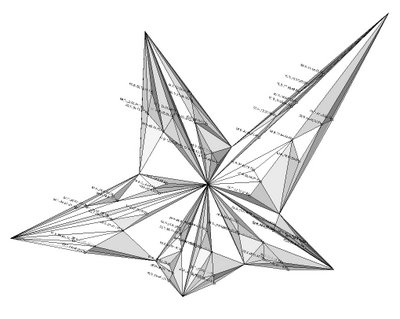
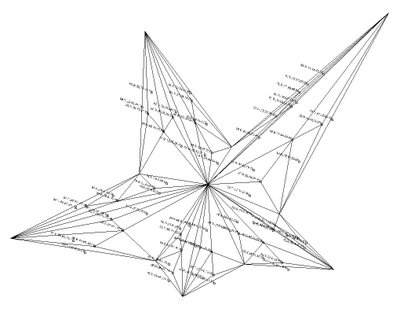
Here is a first code on a research for a set of self similar furnitures based on fractal diamond subdivision...
This routine is similar to a very interesting "Cracking algorythm" developped by Aranda/Larsch (i.e. Terraswarm link).

Sub SubDivDiamond()
' ------------------------------------------------------
' getPts
Dim arrPts00: arrPts00 = Rhino.GetPoints(vbTrue)
Dim dblDeletaHeight: dblDeletaHeight = 0
' ------------------------------------------------------
' LOOP_00
' set firstCentroide
Dim strPoly00: strPoly00 = Rhino.AddPolyline(arrPts00)
Dim arrMP00: arrMP00 = Rhino.CurveAreaCentroid(strPoly00)
' set firstCentroide_Height
Dim arrMP00_deltaHeight: arrMP00_deltaHeight = Array( arrMP00(0)(0), arrMP00(0)(1), arrMP00(0)(2) + dblDeletaHeight )
arrMP00(0) = arrMP00_deltaHeight
' set arrays of 3pts each
Dim i, arrPtsTank00()
For i = 1 To UBound (arrPts00)
ReDim Preserve arrPtsTank00(i-1)
arrPtsTank00(i-1) = Array( arrMP00(0), arrPts00(i-1), arrPts00(i) )
Next
' ------------------------------------------------------


' LOOPS
Dim n1, n2, n3
Dim arrPtsTank01(), arrPtsTank02(), arrPtsTank03()

For n1 = 0 To UBound(arrPtsTank00)
ReDim Preserve arrPtsTank01(n1)
arrPtsTank01(n1) = Subdiv (arrPtsTank00(n1))

For n2 = 0 To UBound(arrPtsTank01(n1))
ReDim Preserve arrPtsTank02(n2)
arrPtsTank02(n2) = Subdiv (arrPtsTank01(n1)(n2))
'Rhino.addCurve arrPtsTank01(n1)(n2)

For n3 = 0 To UBound(arrPtsTank02(n2))
ReDim Preserve arrPtsTank03(n3)
arrPtsTank03(n3) = Subdiv (arrPtsTank02(n2)(n3))
Next

Next

Next

' ------------------------------------------------------
End Sub
SubDivDiamond
' ------------------------------------------------------

' ------------------------------------------------------
Function Subdiv(arrPtsInput)
Dim j
Dim arrPtsTank()
Dim dblDeletaHeight2: dblDeletaHeight2 = -15

Dim strPoly: strPoly = Rhino.AddPolyline (Array (arrPtsInput(0),arrPtsInput(1),arrPtsInput(2), arrPtsInput(0)) )
Dim arrMP: arrMP = Rhino.CurveAreaCentroid(strPoly)
' Centroide_Height
Dim arrMP_deltaHeight: arrMP_deltaHeight = Array( arrMP(0)(0), arrMP(0)(1), arrMP(0)(2) + dblDeletaHeight2 )
arrMP(0) = arrMP_deltaHeight
' Centroide_Annotation
Dim arrPtCentroid: arrPtCentroid = Rhino.AddPoint (arrMP(0))
Rhino.AddText Rhino.Pt2Str(arrMP(0),2), arrMP(0), 1

For j = 1 To UBound (arrPtsInput)
' set Arrays of 3pts each
ReDim Preserve arrPtsTank(j-1)
arrPtsTank(j-1) = Array( arrMP(0), arrPtsInput(j-1), arrPtsInput(j) )
' addSrf
Rhino.AddSrfPt arrPtsTank(j-1)
Next

Subdiv = arrPtsTank
End Function
' ------------------------------------------------------

Table based on SubDiv code...
The foots are folded plates based on lowered centroides (vertical displacement of gravity centers) for each generation of created triangles...