070122_rh4_Voronoi&Arcs

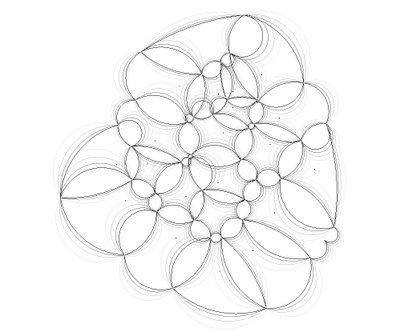
"VORONARC"
Those two drawings are part of a speculative research onto Voronoi and Arcs; the serie is looking beyond the trend of Voronoi diagrams and their most common graphical output as cellular aggragates (now used within every architectural school!); here encoded arcs are used to illustrate possible structural moments within each cell boundaries segments...
ARC (wikipedia.org)
In Euclidean geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of a circle. If the arc segment occupies a great circle (or great ellipse), it is considered a great-arc segment.
The length of a circular arc of a circle with radius r and subtending an angle θ (measured in radians) with the circle centre, equals θr. For an angle α measured in degrees, the size in radians is given by (α/180°) × π, and so the arc length equals then (α/180°)πr.
Tips'n tricks : (ie: David Rutten's Rhinoscript101 on Arc)
Function AddArcDir(ByVal ptStart, ByVal ptEnd, ByVal vecDir)
AddArcDir = Null
Dim vecBase : vecBase = Rhino.PointSubtract(ptEnd, ptStart)
If Rhino.VectorLength(vecBase) = 0.0 Then Exit Function
If Rhino.IsVectorParallelTo(vecBase, vecDir) Then Exit Function
vecBase = Rhino.VectorUnitize(vecBase)
vecDir = Rhino.VectorUnitize(vecDir)
Dim vecBisector : vecBisector = Rhino.VectorAdd(vecDir, vecBase)
vecBisector = Rhino.VectorUnitize(vecBisector)
Dim dotProd : dotProd = Rhino.VectorDotProduct(vecBisector, vecDir)
Dim midLength : midLength = (0.5 * Rhino.Distance(ptStart, ptEnd)) / dotProd
vecBisector = Rhino.VectorScale(vecBisector, midLength)
AddArcDir = Rhino.AddArc3Pt(ptStart, ptEnd, Rhino.PointAdd(ptStart, vecBisector))
End Function
Labels: Arc, rhinoscript, Voronoi


<< Home