Rh4_060719_SubDiv_Progress...
---------FRACTAL---------
The term fractal was coined in 1975 by Benoît Mandelbrot, from the Latin fractus, meaning "broken" or "fractured." In colloquial usage, a fractal is a shape that is recursively constructed or self-similar, that is, a shape that appears similar at all scales of magnification and is therefore often referred to as "infinitely complex." Mathematicians avoid giving the strict definition and prefer to call 'fractal a geometric object that usually.
GENERATING FRACTALS
Three common techniques for generating fractals are:
1. ITERATED FUNCTION SYSTEMS — These have a fixed geometric replacement rule. Cantor set, Sierpinski carpet, Sierpinski gasket, Peano curve, Koch snowflake, Harter-Heighway dragon curve, T-Square, Menger sponge, are some examples of such fractals.
2. ESCAPE-TIME FRACTALS — Fractals defined by a recurrence relation at each point in a space (such as the complex plane). Examples of this type are the Mandelbrot set, the Burning Ship fractal and the Lyapunov fractal.
3. RANDOM FRACTALS — Generated by stochastic rather than deterministic processes, for example, fractal landscapes, Lévy flight and the Brownian tree. The latter yields so-called mass- or dendritic fractals, for example, diffusion-limited aggregation or reaction-limited aggregation clusters.
CLASSIFICATION OF FRACTALS
Fractals can also be classified according to their self-similarity. There are three types of self-similarity found in fractals:
1. EXACT SELF-SIMILARITY — This is the strongest type of self-similarity; the fractal appears identical at different scales. Fractals defined by iterated function systems often display exact self-similarity.
2. QUASI SELF-SIMILARITY — This is a loose form of self-similarity; the fractal appears approximately (but not exactly) identical at different scales. Quasi-self-similar fractals contain small copies of the entire fractal in distorted and degenerate forms. Fractals defined by recurrence relations are usually quasi-self-similar but not exactly self-similar.
3. STATISTICAL SELF-SIMILARITY — This is the weakest type of self-similarity; the fractal has numerical or statistical measures which are preserved across scales. Most reasonable definitions of "fractal" trivially imply some form of statistical self-similarity. (Fractal dimension itself is a numerical measure which is preserved across scales.) Random fractals are examples of fractals which are statistically self-similar, but neither exactly nor quasi-self-similar.
'------------------------------------------------------------
"diamonds are for ever..." as should be the such type of structures...
here, the speculation is to carry the load down at the gravity pt for structural stability...
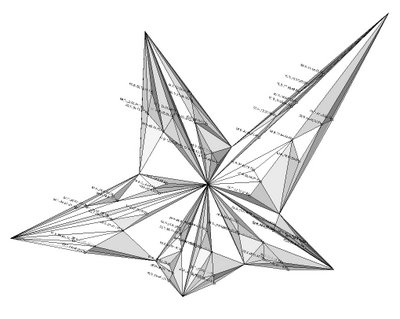
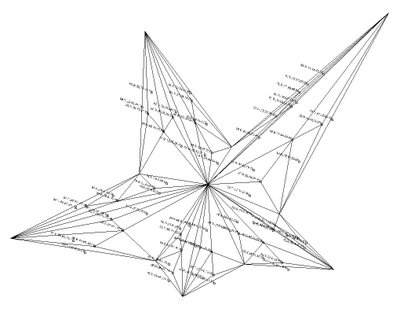
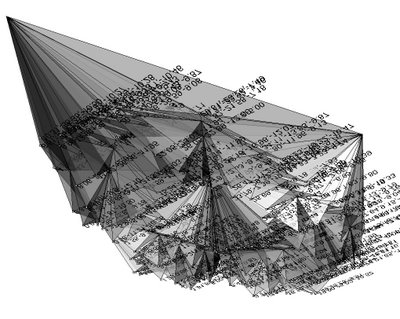
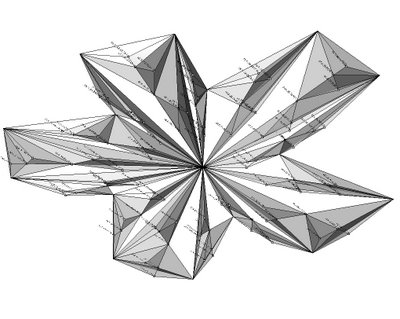
the code is starting from a closed polyline, subdividing the created project surface into triangles (or arrays of 3pts), locating areas centroides, changing their Z value and looping (fractal subdivision)...
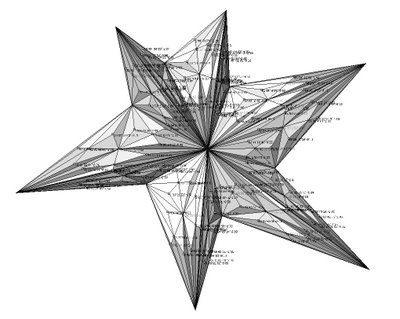

The term fractal was coined in 1975 by Benoît Mandelbrot, from the Latin fractus, meaning "broken" or "fractured." In colloquial usage, a fractal is a shape that is recursively constructed or self-similar, that is, a shape that appears similar at all scales of magnification and is therefore often referred to as "infinitely complex." Mathematicians avoid giving the strict definition and prefer to call 'fractal a geometric object that usually.

GENERATING FRACTALS
Three common techniques for generating fractals are:
1. ITERATED FUNCTION SYSTEMS — These have a fixed geometric replacement rule. Cantor set, Sierpinski carpet, Sierpinski gasket, Peano curve, Koch snowflake, Harter-Heighway dragon curve, T-Square, Menger sponge, are some examples of such fractals.
2. ESCAPE-TIME FRACTALS — Fractals defined by a recurrence relation at each point in a space (such as the complex plane). Examples of this type are the Mandelbrot set, the Burning Ship fractal and the Lyapunov fractal.
3. RANDOM FRACTALS — Generated by stochastic rather than deterministic processes, for example, fractal landscapes, Lévy flight and the Brownian tree. The latter yields so-called mass- or dendritic fractals, for example, diffusion-limited aggregation or reaction-limited aggregation clusters.
CLASSIFICATION OF FRACTALS
Fractals can also be classified according to their self-similarity. There are three types of self-similarity found in fractals:
1. EXACT SELF-SIMILARITY — This is the strongest type of self-similarity; the fractal appears identical at different scales. Fractals defined by iterated function systems often display exact self-similarity.
2. QUASI SELF-SIMILARITY — This is a loose form of self-similarity; the fractal appears approximately (but not exactly) identical at different scales. Quasi-self-similar fractals contain small copies of the entire fractal in distorted and degenerate forms. Fractals defined by recurrence relations are usually quasi-self-similar but not exactly self-similar.
3. STATISTICAL SELF-SIMILARITY — This is the weakest type of self-similarity; the fractal has numerical or statistical measures which are preserved across scales. Most reasonable definitions of "fractal" trivially imply some form of statistical self-similarity. (Fractal dimension itself is a numerical measure which is preserved across scales.) Random fractals are examples of fractals which are statistically self-similar, but neither exactly nor quasi-self-similar.
'------------------------------------------------------------
"diamonds are for ever..." as should be the such type of structures...
here, the speculation is to carry the load down at the gravity pt for structural stability...
the code is starting from a closed polyline, subdividing the created project surface into triangles (or arrays of 3pts), locating areas centroides, changing their Z value and looping (fractal subdivision)...